6. Działania uogólnione
Przedstawione do tej pory operacje (działania) na zbiorach
miały co najwyżej dwa argumenty. Można je jednak uogólnić w
prosty sposób na dowolną, skończoną lub nieskończoną,
liczbę argumentów.
Definicja 1.8
Niech A będzie rodziną zbiorów indeksowaną elementami pewnego zbioru I, A = {Ai : iÎ
I}.
Sumą uogólnioną rodziny zbiorów A nazywamy zbiór
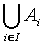
taki, że x należy do tego zbioru wtedy i tylko wtedy,
gdy x jest elementem co najmniej jednego zbioru rodziny A,
x Î
îþ
iÎ
I Ai wttw istnieje takie kÎ
I , że x Î
Ak .
Iloczynem (przecięciem) uogólnionym rodziny zbiorów A nazywamy zbiór
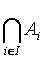
taki, że x należy do tego zbioru wtedy i tylko wtedy, gdy
x jest elementem każdego ze zbiorów rodziny A,
x Î
ìü
iÎ
I Ai wttw dla wszystkich kÎ
I , x Î
Ak .
Oczywiście, gdy I składa się tylko z dwóch indeksów, np. I={1, 2}, to
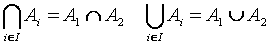
Jeżeli wszystkie zbiory rodziny A należą do tej samej przestrzeni U, to zachodzą uogólnione prawa De Morgana sformułowane w twierdzeniu 1.4.
Twierdzenie 1.4
Dla dowolnej rodziny podzbiorów {Ai : iÎ
I} zbioru U, zachodzą równości
- - îþ
iÎ
I Ai = ìü
iÎ
I (- Ai )
- - ìü
iÎ
I Ai = îþ
iÎ
I (- Ai )
Dowód.
Ad. 1) Załóżmy, że x należy do lewej strony równości (1). Oznacza to, na mocy definicji, że x nie należy do żadnego ze zbiorów Ai. Stąd x należy do każdego z uzupełnień -Ai i w konsekwencji x należy do przecięcia
ìü
iÎ
I (- Ai ).
Ad. 2) Jeśli element x należy do
zbioru -ìü
iÎ
I Ai , to nie należy do przecięcia uogólnionego
ìü
iÎ
I Ai. Zatem, na mocy definicji 1.8, dla pewnego k, x Ï
Ak. Stąd x Î
-Ak, czyli xÎ
îþ
iÎ
I (- Ai ).J
Przykład 1.10
- Niech Ai = {x Î
R : x < i} dla wszystkich liczb naturalnych i. Wtedy
îþ
iÎ
I Ai = R, a
ìü
iÎ
I Ai = {x Î
R : x < 0}.
- Niech Bi = {x Î
R : -1/i <x < 1/i}dla wszystkich liczb naturalnych i>0. Wtedy
îþ
iÎ
I Bi = (-1,1), a
ìü
iÎ
I Bi = {0}.
Pytanie 8: Niech {Ai : iÎ
I}będzie indeksowaną rodziną zbiorów pewnej przestrzeni.
Które z wymienionych zależności są, a które nie są prawdziwe?
1. Dla dowolnego kÎ
I, Ak Í
îþ
iÎ
I Ai.
2. Dla dowolnego kÎ
I, Ak Í
ìü
iÎ
I Ai.
3. Dla dowolnego kÎ
I, îþ
iÎ
I Ai Í
Ak.
4. Dla dowolnego kÎ
I,ìü
iÎ
I Ai Í
Ak.
5. ìü
iÎ
I Ai Í
îþ
iÎ
I Ai.
![]()
![]()